Python递归算法及其简单应用

一、递归算法

递归算法是一个相对较抽象的问题，有点像套娃，一开始不怎么好理解。

一旦抓住了核心思路，理解起来就相对容易了。

• 递归问题要点：
  1. 边界条件（终止条件）：否则将无限循环
  2. 子问题必须与原问题结构一致，但是输入规模小于原问题的规模（即要求问题分解和循环计算）
• 递归解题思路：
  1. 假设问题有解，且函数为Fun(p)，p为函数的输入；
  2. 可将原问题分解为为n个子问题，即P1，P2，P3，....Pn
     • 由于原问题的函数为Fun，因此求解各子问题的函数依然为Fun()
     • 子问题对应输入元素个数（规模）要小于原问题的输入元素
  3. 建立子问题的解与原问题的关系：
     • Fun(p)=Fun(P1)+Fun(P2)+Fun(P3)......+Fun(Pn)
     • 根据以上关系得到递归结构
     • 子问题最简形式存在解（边界或终止条件）

二、斐波那契函数

题目简单明了，函数和终止条件已经说明

• 题目：
  1. f(n)=f(n-1)+f(n-2)
  2. f(0)=0 #终止条件1
  3. f(1)=1 #终止条件2

def fib_recursion(n):
    if n<=1:
        return n
    else:
        return fib_recursion(n-1)+fib_recursion(n-2)
if __name__=="__main__":
    for i in range(1,31):
        print(i,fib_recursion(i))

三、回文判断

• 题目：
  1. 正向与反向读都是相同字符串
  2. 如：noon，上海自来水来自海上，黄山落叶松叶落山黄
• 解题思路：
  1. 先假设输入的字符串是回文
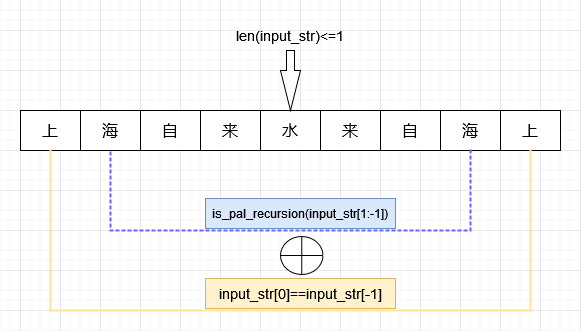
  2. 定义回文函数：is_pal_recursion(input_str)
  3. 分析终止条件：
     • 如果最后只有一个字符，是回文，返回True
     • 如果最后只有零个字符，是回文，返回True
     • len(input_str)<=1，return True
  4. 分解子问题： input_str[0]==input_str[-1] and is_pal_recursion(input_str[1:-1])

def is_pal_recursion(input_str):
    print(input_str)
    if len(input_str) <= 1:
        return True
    else:
        return input_str[0] == input_str[-1] and is_pal_recursion(input_str[1:-1])

if __name__ == "__main__":
    flag = is_pal_recursion("黄山落叶松叶落山黄")
    print(flag)

四、全排列

• 题目：
  1. 输入字符串为N个不相同字符，输出N个字符的全排列
• 解题思路
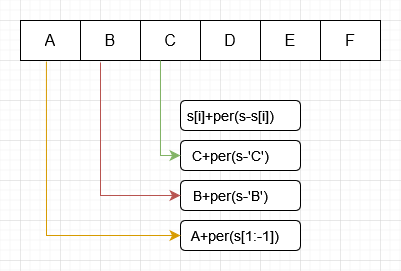
  1. 假设题目存在解，定义函数为：per(s)
  2. 终止条件：s的长度为1，len(s)<=1: return s
  3. 分解子问题：
     • s[i]+per(s-s[i]) #s-s[i]为s[i]以外的字符串，字符串长度为n-1
     • 对字符串s先提取一个，然后对剩余字符串重复调用自身
     • 每一次重复调用自身时，需要将提取的一个字符加上剩余的字符，然后加入到list中

def per(s):
    lens=len(s)
    if lens<=1:
        return s
    else:
        result=[]
        for i in range(lens):
            ch=s[i]
            rest=s[0:i]+s[i+1:lens]
            for j in per(rest):
                result.append(ch+j)
        return result

if __name__=="__main__":
    print(per('abcde'))

五、汉诺塔

• 题目：
  1. 小盘必须在大盘上面
  2. 每次只能移动一个盘子
• 解题思路：
  1. 假设问题有解，定义函数：hanoi(n,src,des,tmp)
  2. 边界条件：柱子上只有一个盘子，此时仅需移动一个盘子即可
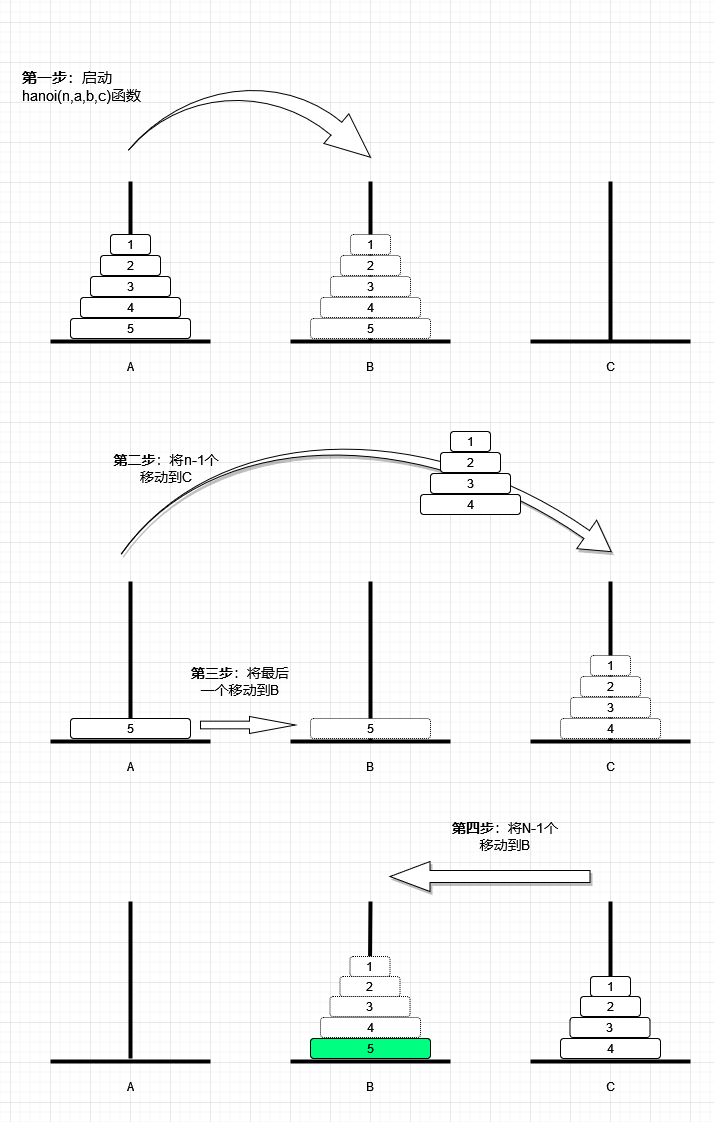
  3. 第一步：启动hanoi函数
  4. 第二步：将n-1个盘子移动到临时柱子（tmp）上；
  5. 第三步：将底部盘子（第n个盘子）移动到目标柱子上；
  6. 第四步：重复调用递归函数，将n-1个盘子移动到目标柱子上。

step = 1

def hanoi(num, src, des, tmp):
    if num <= 1:
        movSingle(src, des)
    else:
        hanoi(num - 1, src, tmp, des)
        movSingle(src, des)
        hanoi(num - 1, tmp, des, src)

def movSingle(src, des):
    global step  # 声明为global，否则cannot access local variable 'step' where it is not associated with a value
    disk = src[0].pop()
    print("第" + str(step) + "步:从" + src[1] + "柱移动" + str(disk) + "盘到" + des[1] + "柱")
    step += 1
    des[0].append(disk)

if __name__ == "__main__":
    a = ([6, 5, 4, 3, 2, 1], "A")
    b = ([], "B")
    c = ([], "C")
    hanoi(len(a[0]), a, b, c)