Python二叉树列表表示

在前一节：Python二叉树遍历，介绍二叉树的遍历操作是以链表方式进行的，本次介绍以列表下操作，在以列表表示二叉树时，就是上一节中“列表转换为二叉树”的思路。

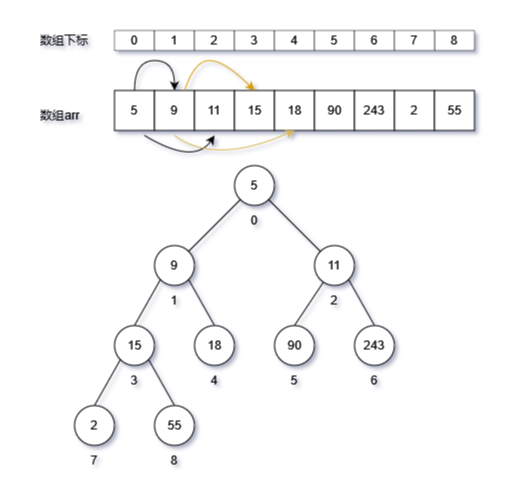
在二叉树的遍历中，介绍了将列表转换为二叉树（链表形式），其中介绍了左右子节点的计算公式：

• 左节点下标：i×2+1
• 右节点下标：i×2+2

本介绍主要依据以上两个公式展开，同时介绍由子节点计算负节点。

需要注意的是，二叉树多数情况下不是完美二叉树或者完全二叉树，节点可能会只有一个子节点，那么另一个子节点需要用None存储在列表中。

一、基本方法

• 获取根节点左节点下标

    def getLeft(self, i):
        return i * 2 + 1
  

• 获取节点父节点下标

  # 注意计算公式
    def getPar(self, i):
        return (i - 1) // 2
  

• 获取节点值

  # 注：是>=
    def getVar(self, i):
        if i < 0 or i >= self.size():
            return None
        return self.__tree[i]
  

• 获取左节点值

    def getLeftVar(self, i):
        return self.getVar(self.getLeft(i))
  

  二、广度优先遍历

用列表表示二叉树，本身就是将列表按层来存储和表示列表，因此，直接返回列表的值即可。

但是使用过程中，需要注意二叉树中的只有一个子节点的情况，此时需要过滤掉值为None的节点。

# 广度优先遍历，即返回数组即可
    def bfs_travel(self):
        for i in range(self.size()):
            if self.__tree[i] is not None:
                self.__res.append(self.getVar(i))

三、深度优先遍历

深度优先遍历，同上一节链表的使用方式相同，通过递归的方式来实现 边界（终止）条件：子节点的元素为None 然后根据前序、中序、后序要求，访问根节点、左节点、右节点 这里访问左右子节点的方式不同，不再通过链表指针实现，二是通过计算左右子节点在列表的下标实现。

1. 前序遍历

   # 深度优先遍历-前序方式
    # 当元素为None，表明无子节点，回溯返回。这里无须再次判断是否数组越界，因元素为None，就是无子树了，不进行下一步，回溯即可。
    def dfs_pre(self, i):
        if self.getVar(i) is None:
            return
        self.__res.append(self.getVar(i))
        self.dfs_pre(self.getLeft(i))
        self.dfs_pre(self.getRight(i))
   

2. 中序遍历

    def dfs_mid(self, i):
        if self.getVar(i) is None:
            return
        self.dfs_mid(self.getLeft(i))
        self.__res.append(self.getVar(i))
        self.dfs_mid(self.getRight(i))
   

四、完整代码

class BinaryTreeList:
    def __init__(self, arr):
        self.__tree = list(arr)
        self.__res = []

    def size(self):
        return len(self.__tree)

    # 注：是>=
    def getVar(self, i):
        if i < 0 or i >= self.size():
            return None
        return self.__tree[i]

    def getLeft(self, i):
        return i * 2 + 1

    def getRight(self, i):
        return i * 2 + 2

    # 注意计算公式
    def getPar(self, i):
        return (i - 1) // 2

    def getLeftVar(self, i):
        return self.getVar(self.getLeft(i))

    def getRightVar(self, i):
        return self.getVar(self.getRight(i))

    def getParVar(self, i):
        return self.getVar(self.getPar(i))

    # 广度优先遍历，即返回数组即可
    def bfs_travel(self):
        for i in range(self.size()):
            if self.__tree[i] is not None:
                self.__res.append(self.getVar(i))


    # 深度优先遍历-前序方式
    # 当元素为None，表明无子节点，回溯返回。这里无须再次判断是否数组越界，因元素为None，就是无子树了，不进行下一步，回溯即可。
    def dfs_pre(self, i):
        if self.getVar(i) is None:
            return
        self.__res.append(self.getVar(i))
        self.dfs_pre(self.getLeft(i))
        self.dfs_pre(self.getRight(i))

    def dfs_mid(self, i):
        if self.getVar(i) is None:
            return
        self.dfs_mid(self.getLeft(i))
        self.__res.append(self.getVar(i))
        self.dfs_mid(self.getRight(i))

    # res定义在构造函数中，如果不清空，多种方法append后，列表内部元素会不断增加
    def clear(self):
        self.__res = []

    def getRes(self):
        return self.__res