Python二叉树的遍历
一、二叉树几个概念
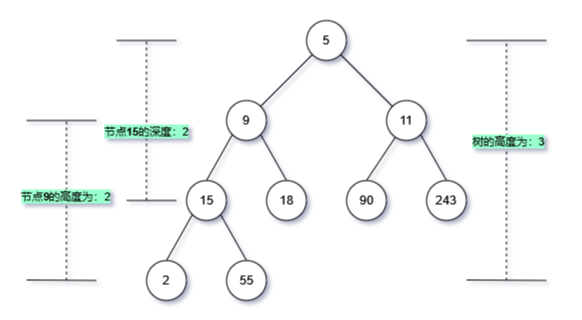
注意区分几个概念:
- 二叉树的高度与层;
- 二叉树的高度是从最底部起算,而深度是从根节点起算;
基本术语
- 节点所在的层 level:从顶至底递增,根节点所在层为 1
- 节点的度 degree:节点的子节点的数量。在二叉树中,度的取值范围是[ 0、1、2] 。即节点所拥有叶子节点的数量
- 二叉树的高度 height:从根节点到最远叶节点所经过的边的数量。
- 节点的深度 depth:从根节点到该节点所经过的边的数量。
- 节点的高度 height:从距离该节点最远的叶节点到该节点所经过的边的数量。
树的类型
- 完美二叉树:所有层的节点都被完全填满,满二叉树,叶节点的度为0,其余所有节点的度都为2;若树的高度为h,则节点总数为
2^(h+1)-1,如一个高度h=3的满二叉树,即有根节点到底节点共有4层,一共有15个节点(第一层1个,第二层2个,第三层4个,第四层8个) - 完全二叉树:只有最底层的节点未被填满,且最底层节点尽量靠左填充。
- 完满二叉树:除了叶节点之外,其余所有节点都有两个子节点,即节点的度,要么为0,要么为2
- 平衡二叉树:任意节点的左子树和右子树的高度之差的绝对值不超过 1
二、列表转换为二叉树
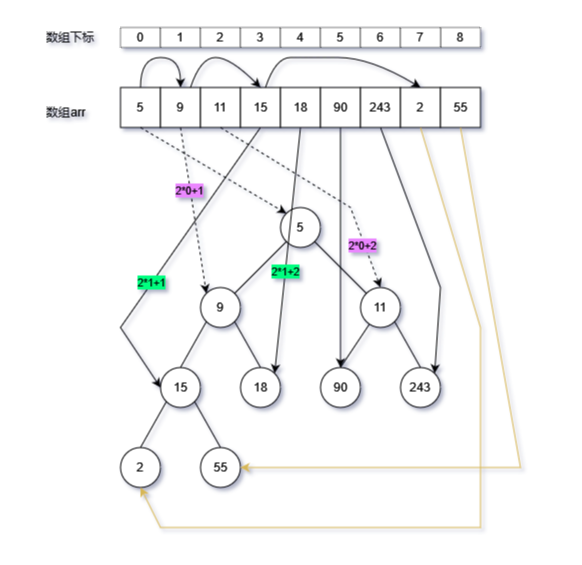
将列表元素按照层顺序,逐层填满二叉树,即转换之后的二叉树是一个完全二叉树 计算公式:
- 当前元素的下标为i,如:第0个元素;
- 其左节点的下标为i×2+1,如:第0个元素的,左节点下标为1;
- 其右节点的效标为i×2+2,如:第0个元素,右节点的下标为2;
- 整体上通过递归方式实现,边界(返回)条件为列表下标越界,或者元素为None;
- 由于要获取元素的左、右两个子节点,因此递归中需要两次调用函数本身,获取左右子节点
# 使用递归方式,将list转换为二叉树,按层的顺序实现转换
# 先判断arr的下标start是否越界,然后再新建节点
def create_btree(arr, start):
if start < 0 or start >= len(arr) or arr[start] is None:
return None
root = TreeNode(arr[start])
root.left = create_btree(arr, start * 2 + 1)
root.right = create_btree(arr, start * 2 + 2)
return root
三、广度优先遍历
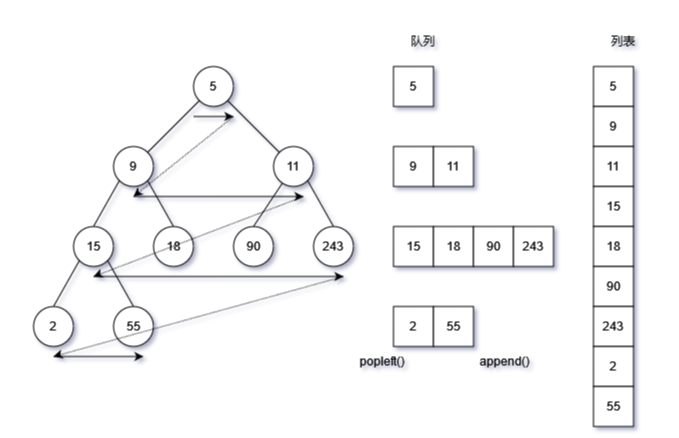
广度优先(breadth-first traversal),即按层遍历二叉树的所有节点,逐层访问全部节点的方式
实现方式:(队列)
- 使用标准库(collections)中的deque双向链表类作为列表
- 使用while循环,当队列为None是终止循环
- 读取根节点,同时获取左右子节点,按照顺序将左右节点加入(append)队列;append
- 弹出(popleft)队列中节点,同时获取其左右自节点,按照顺序将左右节点加入队列;
- 弹出队列的节点时,将节点元素内容存入列表。
# 广度优先(breadth-first traversal)方式遍历二叉树
# 以队列方式实现,按层进行遍历
def bfs_travel(root):
res = []
queue = deque()
queue.append(root)
while queue:
node: TreeNode = queue.popleft()
res.append(node.val)
if node.left is not None:
queue.append(node.left)
if node.right is not None:
queue.append(node.right)
return res
四、深度优先遍历
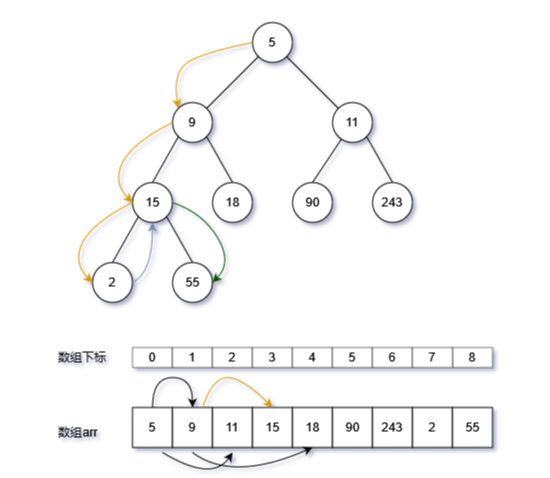
深度优先分为前序、中序以及后序方式,区分的依据为访问根节点的顺序,前序即为先访问根节点,然后依次访问左右节点;中序为先访问左节点,然后依次访问根、右节点;后序为依次访问左节点、右节点、根节点。 二叉树搜索即为中序方式,左节点<根节点<右节点 深度优先的实现方式依赖于递归
- 边界(返回)条件:节点为None
- 然后依次调用函数本身,访问左、右节点,根据前序、中序、后序需要,访问根节点元素
前序遍历
res_pre=[] # 深度优先就是使用递归方式 # 深度优先(depth-first search):前序遍历 # 前序遍历:根节点-左子树-右子树 # 中序遍历:左子树-根节点-右子树 # 后续遍历:左子树-右子树-根节点 def dfs_pre(root:TreeNode): # 递归边界(返回条件):节点为None if root is None: return # 访问根节点 res_pre.append(root.val) # 递归处理左子树 dfs_pre(root=root.left) # 递归处理右子树 dfs_pre(root=root.right)中序遍历
res_mid=[] # 深度优先遍历:中序方式,左子树-根节点-右子树 # 如果是一个有序的二叉树,中序遍历出来的元素就是一个有序的列表,左节点< 中节点(根节点) < 右节点 def dfs_mid(root:TreeNode): if root is None: return dfs_mid(root=root.left) res_mid.append(root.val) dfs_mid(root=root.right)
五、完整代码
from typing import Optional
# deque是collections中的双向链表实现
from collections import deque
class TreeNode:
def __init__(self, val: int):
self.val: int = val
self.left: Optional[TreeNode] = None
self.right: Optional[TreeNode] = None
# 使用递归方式,将list转换为二叉树,按层的顺序实现转换
# 先判断arr的下标start是否越界,然后再新建节点
def create_btree(arr, start):
if start < 0 or start >= len(arr) or arr[start] is None:
return None
root = TreeNode(arr[start])
root.left = create_btree(arr, start * 2 + 1)
root.right = create_btree(arr, start * 2 + 2)
return root
# 广度优先(breadth-first traversal)方式遍历二叉树
# 以队列方式实现,按层进行遍历
def bfs_travel(root):
res = []
queue = deque()
queue.append(root)
while queue:
node: TreeNode = queue.popleft()
res.append(node.val)
if node.left is not None:
queue.append(node.left)
if node.right is not None:
queue.append(node.right)
return res
res_pre=[]
# 深度优先就是使用递归方式
# 深度优先(depth-first search):前序遍历
# 前序遍历:根节点-左子树-右子树
# 中序遍历:左子树-根节点-右子树
# 后续遍历:左子树-右子树-根节点
def dfs_pre(root:TreeNode):
# 递归边界(返回条件):节点为None
if root is None:
return
# 访问根节点
res_pre.append(root.val)
# 递归处理左子树
dfs_pre(root=root.left)
# 递归处理右子树
dfs_pre(root=root.right)
res_mid=[]
# 深度优先遍历:中序方式,左子树-根节点-右子树
# 如果是一个有序的二叉树,中序遍历出来的元素就是一个有序的列表,左节点< 中节点(根节点) < 右节点
def dfs_mid(root:TreeNode):
if root is None:
return
dfs_mid(root=root.left)
res_mid.append(root.val)
dfs_mid(root=root.right)