Python排序算法-堆排序

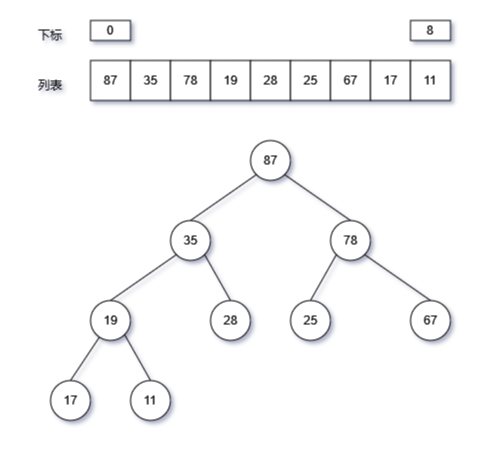
堆排序就是一个不断弹出堆顶元素（堆中的最大值），堆同时在缩小，然后不断堆化和弹出堆顶元素进行排序。

堆化的理解，请看前面小节：Python堆操作

一、实现思路

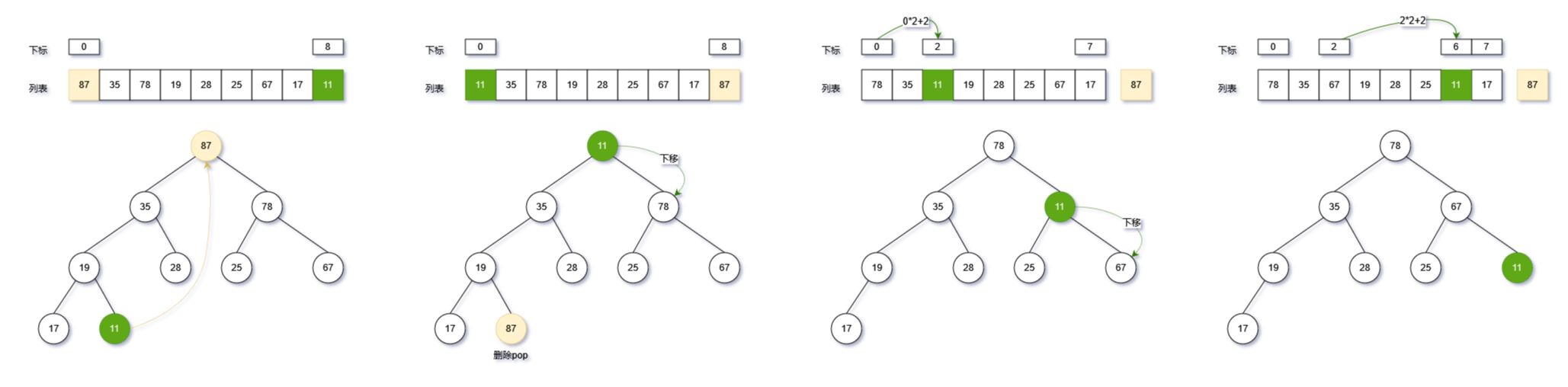
1. 首先对列表元素进行建堆，此时堆顶元素就是列表最大的元素；
2. 弹出堆顶元素（堆中最大值）：弹出堆顶元素时，是将堆顶元素（nums[0]）与列表最后的元素互换（nums[len-1]）。nums[i], nums[0] = nums[0], nums[i]
3. 然后循环执行以上两个步骤，堆缩小的堆不断弹出堆顶元素。

二、注意要点

1. 注意堆化（shift_down）过程中while循环的终止条件：互换后堆顶仍为最大值或者i无左右子顶点；

2. 注意列表长度的变化，在堆排序函数中，列表长度在缩小，取得堆顶元素后，列表下标i变为缩小后堆的长度。

   for i in range(len(nums) - 1, 0, -1):
       nums[i], nums[0] = nums[0], nums[i]
       shift_down(nums, i, 0)
   

3. 注意for i in range(len(nums) - 1, 0, -1)堆缩小后，列表下标的最小值为1，这是因为n-1个元素排序完毕后，堆中的最后一个元素必然是最小的。

4. 注意建堆的过程，此处建堆与之前的从上到下的建堆略有不同，此处为从下到上的建堆。

   # 建堆操作
   for i in range(len(nums) // 2 - 1, -1, -1):
       shift_down(nums, len(nums), i)
   

# 堆排序
# l:堆的长度（列表长度）
# i：堆的顶点（也可以是左右子堆的顶点，随着向下移动，顶点在向下移动）
def shift_down(nums: list[int], l: int, i: int):
    while True:
        left = i * 2 + 1
        right = i * 2 + 2
        # 最大值先指向堆顶，然后与左右子堆比较，进行堆化
        mx = i
        if left < l and nums[mx] < nums[left]:
            mx = left
        if right < l and nums[mx] < nums[right]:
            mx = right
        # 当顶点指针移动到下边叶子节点时，无左右子顶点，表示遍历完毕，跳出循环，说明向下移动全部完成，或者i顶点本身就比左右子堆节点大
        if mx == i:
            break
        nums[i], nums[mx] = nums[mx], nums[i]
        # 堆顶顶点与左右子顶点互换后，堆顶向下移动（移向左右子顶点最大的顶点）
        i = mx


def heap_sort(nums: list[int]):
    # 建堆操作
    for i in range(len(nums) // 2 - 1, -1, -1):
        shift_down(nums, len(nums), i)

    # 堆排序操作，先将列表堆顶与列表最后一个元素互换，然后对堆顶元素向下移动进行堆化
    # 注意i变量，0和i元素互换取得最大元素后，i相当于后面堆的长度
    for i in range(len(nums) - 1, 0, -1):
        nums[i], nums[0] = nums[0], nums[i]
        shift_down(nums, i, 0)


if __name__ == '__main__':
    nums = [62, 65, 51, 15, 30, 63, 37, 8, 55, 70, 13, 84, 46, 44, 86, 11, 91, 10, 47, 3, 96, 9, 36, 54, 24, 72,
            29, 45]
    heap_sort(nums)
    print(nums)