Python分治算法应用-构建二叉树
- 问题

根据二叉树的深度遍历前序列表(pre_list)和中序列表(mid_list),构建对应的二叉树。如:
- 前序列表:
pre_list = [5, 9, 15, 2, 55, 18, 11, 90, 243]- 中序列表:
mid_list = [2, 15, 55, 9, 18, 5, 90, 11, 243]- 生成二叉树的广度优先遍历结果应为:
bfs_list = [5, 9, 11, 15, 18, 90, 243, 2, 55],可以作为验证。
一、分治算法基本思路
在学习二叉树的深度遍历以及归并排序、快速排序等小节时,使用的就是分而治之的思路。通常分治法通过递归实现,整体上包含两个部分:划分问题和合并问题
- 划分问题:将题目问题划分为规模较小的问题;按照递归的基本原理,小问题与原问题结构是一致的;直到小的问题无法再划分(达到边界条件)时,停止划分
- 合并问题:当达到边界条件时,从下到上返回,开始合并小问题。
一个问题是否适合使用分治解决,通常可以参考以下几个判断依据。
- 问题可以分解:原问题可以分解成规模更小、类似的子问题,以及能够以相同方式递归地进行划分。
- 子问题是独立的:子问题之间没有重叠,互不依赖,可以独立解决。
- 子问题的解可以合并:原问题的解通过合并子问题的解得来。
二、解题步骤
根据分治算法的基本思路,下面解决构建二叉树:
- 在前序列表中,我们知道根节点在列表的最左侧,可以用下标i表示;
- 同理,在前序列表中,左子树的根节点紧跟着根节点,可以用下标i+1表示;
- 下面就要推算右子树的根节点,这里要稍微复杂,直接给出结果,如下表
| 树 | 根节点索引pre_list | 子树的列表区间mid_list |
|---|---|---|
| 当前树 | i | [left,right] |
| 左子树 | i+1 | [left,m-1] |
| 右子树 | i+1+(t-left) | [t+1,right] |
- t为当前树根节点在中序列表mid_list的索引(下标)
- t-left即为左子树元素的节点的个数。因为m在中序列表mid_list中的的位置,代表中t左侧全部为左子树节点,t的右侧全部为右子树的节点,因此t-left表示左子树节点的数量。
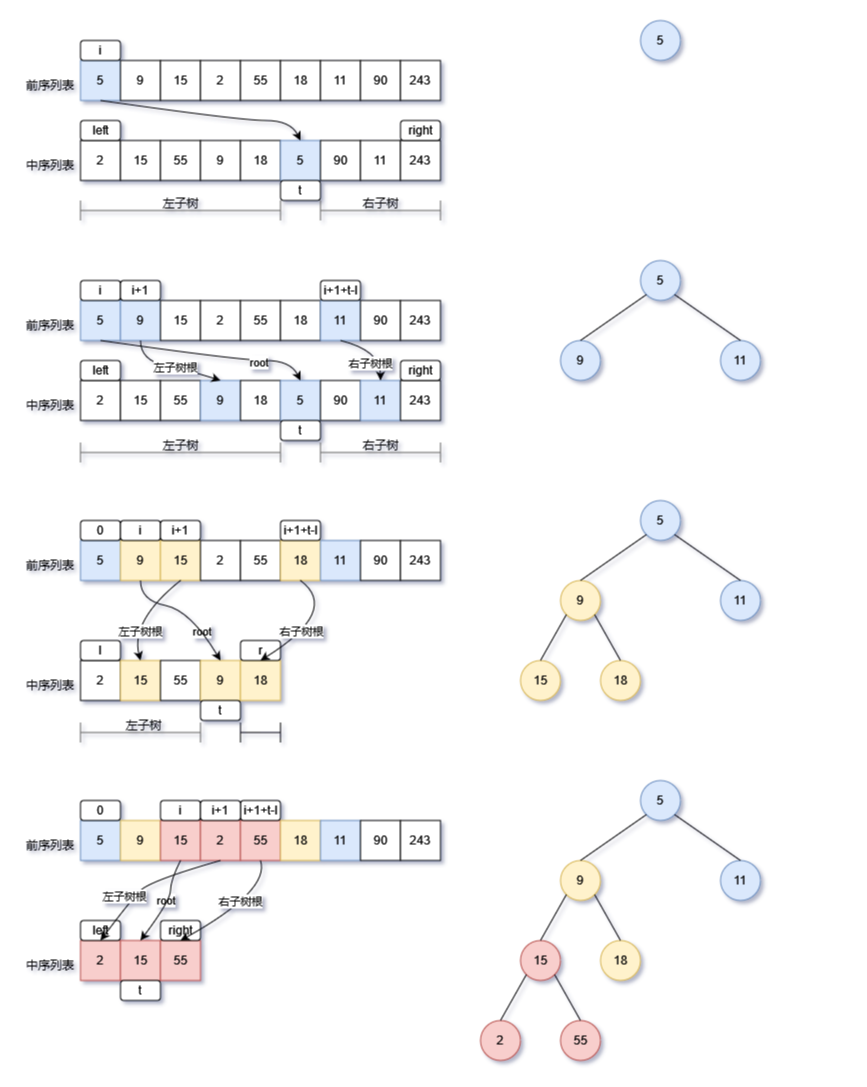
实现步骤
- 先通过i在前序列表pre_list,初始化根节点root;
- 通过i+1在前序列表pre_list,可以构建左子树根节点,然后连接在根节点的left指针上;
- 通过根节点元素值,获取在中序列表mid_list的索引t,
- 通过i+1+(t-left)在前序列表pre_list,可以构建右子树根节点,然后连接在根节点的right指针上;
- 让后通过递归的方式,继续探索左右子树,不断的向下构建子树和节点。
- 递归的边界条件:节点为叶子节点,无左右子树,即此时子树的列表区间中,left和right指向同一个节点(叶子节点),
right-left==0
# 使用递归的分治策略,根据前序列表和中序字典,逐层向下递归,向上返回的方式构建二叉树,可以通过return上部的print查看构建过程
# 参数说明:
# pre_list:深度优先前序遍历列表
# mid_dict:深度优先中序遍历列表生成的列表
# root_index:前序列表中根节点下标
# left:中序列表左侧元素下标
# right:中序列表右侧元素下标
def dfs(pre_list:list[int],mid_dict:dict[int,int],root_index,left,right):
# 当前节点为叶子节点,right和left指向同一个节点
if right-left<0:
return None
root=TreeNode(pre_list[root_index])
# 通过前序列表元素值,在中序列表中获取下标
t=mid_dict[pre_list[root_index]]
root.left=dfs(pre_list,mid_dict,root_index+1,left,t-1)
root.right=dfs(pre_list,mid_dict,root_index+1+t-left,t+1,right)
print(bfs_travel(root))
return root
三、注意要点
- 要理解t-left的含义;
- 递归的边界条件是当前节点为叶子节点,此时无法构建左右次数,因此
if right-left<0: return None - 在中序列表中获取根节点的索引,先将中序列表转换为字典dict,将元素值作为健,元素的索引作为值,这样可以通过元素值获取到中学列表的索引t,
t=mid_dict[pre_list[root_index]] - 列表转换为字典的用法如下:
mid_dict = {val: index for index, val in enumerate(mid_list)}
四、全部代码
from collections import deque
# 分治算法应用:
# 构建二叉树
# 根据深度优先前序遍历列表和中序遍历列表,还原二叉树
# 树节点类
class TreeNode:
def __init__(self, val: int):
self.val = val
self.left: TreeNode = None
self.right: TreeNode = None
# 以深度优先的方式构建二叉树
# 使用递归的分治策略,根据前序列表和中序字典,逐层向下递归,向上返回的方式构建二叉树,可以通过return上部的print查看构建过程
# 参数说明:
# pre_list:深度优先前序遍历列表
# mid_dict:深度优先中序遍历列表生成的列表
# root_index:前序列表中根节点下标
# left:中序列表左侧元素下标
# right:中序列表右侧元素下标
def dfs(pre_list:list[int],mid_dict:dict[int,int],root_index,left,right):
# 当前节点为叶子节点,right和left指向同一个节点
if right-left<0:
return None
root=TreeNode(pre_list[root_index])
# 通过前序列表元素值,在中序列表中获取下标
t=mid_dict[pre_list[root_index]]
root.left=dfs(pre_list,mid_dict,root_index+1,left,t-1)
root.right=dfs(pre_list,mid_dict,root_index+1+t-left,t+1,right)
print(bfs_travel(root))
return root
def build_tree(pre_list: list[int], mid_list: list[int]):
# 将列表转换为字典,且将列表的值作为健,下标作为键值,后续需要通过键值查找到列表的下标,此下标即为m,用于后续计算左右子节点的首尾下标,以及右子树根节点下标
mid_dict = {val: index for index, val in enumerate(mid_list)}
root=dfs(pre_list,mid_dict,0,0,len(pre_list)-1)
return root
def bfs_travel(root):
res = []
queue = deque()
queue.append(root)
while queue:
node: TreeNode = queue.popleft()
res.append(node.val)
if node.left is not None:
queue.append(node.left)
if node.right is not None:
queue.append(node.right)
return res
if __name__ == '__main__':
# bfs_list = [5, 9, 11, 15, 18, 90, 243, 2, 55]
pre_list = [5, 9, 15, 2, 55, 18, 11, 90, 243]
mid_list = [2, 15, 55, 9, 18, 5, 90, 11, 243]
root=build_tree(pre_list,mid_list)
res=bfs_travel(root)
print(res)