Python二叉搜索树操作

二叉搜索树，可以理解为一个有序二叉树，其要求为：左子树节点的值<根节点的值<右子树节点的值，即按照深度优先中序遍历方式出来的列表，是一个有序列表。

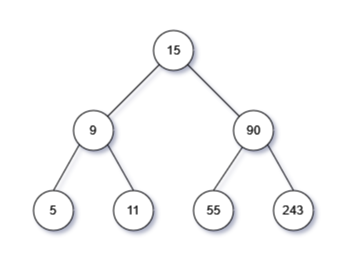
一、遍历二叉树

二叉搜索树的遍历同二叉树相同，可以广度优先，也可以深度优先。

这里重新实现了两种遍历方式，目的是在测试的时候，可以输出二叉树的内容。

广度优先遍历

使用队列实现

# 广度优先遍历
    def bfs(self):
        self.__res=[]
        queue = deque()
        queue.append(self.__root)
        while queue:
            node: TreeNode = queue.popleft()
            self.__res.append(node.val)
            if node.left is not None:
                queue.append(node.left)
            if node.right is not None:
                queue.append(node.right)
        return self.__res

深度优先遍历

使用递归实现

注意，这里借用别人写的一种方式，注意区分dfs函数中if的写法

# 深度优先搜索
    # 这一段是看了别人的写法，很有意思
    # 注意if判断的位置和含义
    def dfs(self,node,order):
        cur = node
        if node is None:
            return
        if order=='pre':
            self.__res.append(cur.val)
        self.dfs(cur.left,order)
        if order=='mid':
            self.__res.append(cur.val)
        self.dfs(cur.right,order)
        if order=='post':
            self.__res.append(cur.val)

    # 深度优先遍历-中序
    # 中序遍历，应该返回一个有序的列表
    def dfs_mid(self):
        cur=self.__root
        self.__res=[]
        self.dfs(cur,'mid')
        return self.__res

    def dfs_pre(self):
        cur=self.__root
        self.__res=[]
        self.dfs(cur,'pre')
        return self.__res

二、搜索节点

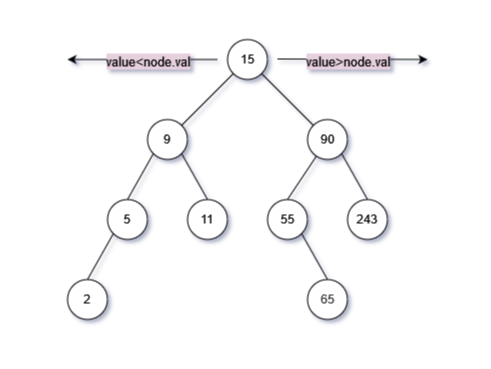
二叉搜索树本身就是一个有序的树，当查找内容小于根节点时，进入左子树；当查找内容大于根节时，进入右子树。

value>cur.val，进入右子树继续搜索，cur=cur.right

value<cur.val，进入左子树继续搜索，cur=cur.left

在遍历整个树的过程中，类似一种深度优先的方式向下前进。

注意这里while循环，如果在循环中找到内容，即返回True；如果在循环中未找到内容，则循环结束后返回False，即未找到内容。

# 当value> 当前节点，跳至当前节点的右子节点
    # 当value< 当前节点，跳至当前节点的左子节点
    # 在while循环中，如果相等则返回True，如果while循环结束仍未跳出循环，说明未找到，则在while循环外返回False
    def search(self, value)->bool:
        cur = self.__root
        while cur is not None:
            if cur.val < value:
                cur = cur.right
            elif cur.val > value:
                cur = cur.left
            else:
                return True
        return False

三、插入节点

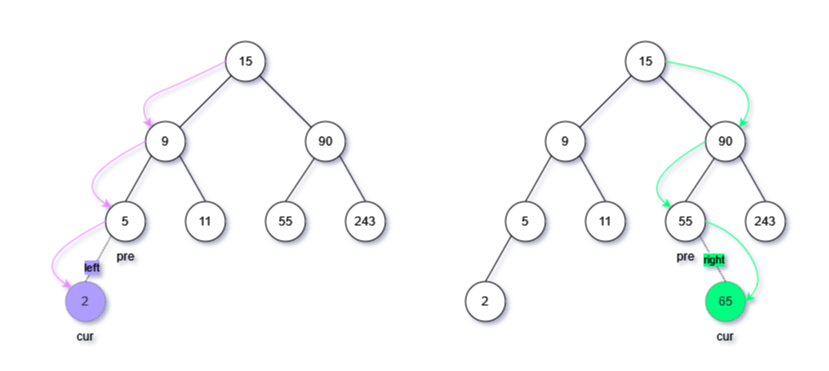
为了保证左子树 < 根节点 < 右子树成立，插入的新节点始终为叶子节点，即在二叉树的底部，有了这个思路，插入就容易理解了。

实现方式：

while循环中，按照深度优先的方式进行搜索，直到cur==None（空节点说明找到父节点的位置了），表明到达最底部，跳出循环；

判断插入元素与父节点的大小，选择插入方向

注意点：

需要定义两个指针变量：pre（记录父节点）和cur（记录当前节点）

当cur为None时，说明已经到二叉树的底部，此时pre指向的是父节点的位置，新节点挂在下面

需要判断插入的节点是否已经在二叉树中存在，如果已经存在，则无须其他操作，退出函数即可return

需要判断树是否为空None，如果是空树，直接将内容填入根即可self.__root=TreeNode(value)

# 考虑两种情况，数为空None和非空，为空则建立一个新节点，然后root指向即可
    # 树非空时，则根据搜索的原理，沿着路径向下走，直到空节点（cur），此时pre为父节点
    # 判断value与pre节点的大小，然后在左右插入节点。
    def insert(self, value):
        if self.__root is None:
            self.__root=TreeNode(value)
            return
        cur=self.__root
        pre=None
        while cur is not None:
            if cur.val==value:
                return
            pre=cur
            if cur.val<value:
                cur=cur.right
            else:
                cur=cur.left

        node=TreeNode(value)
        if pre.val<value:
            pre.right=node
        else:
            pre.left=node

四、删除节点

相对来讲，删除节点比较复杂，考虑的情况较多。

判断删除元素的类型：无叶子节点，只有一个叶子节点的节点，有两个节点的节点。即考虑节点的度degree

需要判断树是否为空self.__root is None

需要判断删除的元素，在二叉树中是否存在，如不存在即返回False

删除节点为无叶子节点（节点的度为0）

无叶子节点时，此种情况最容易，将此节点的父节点left或right指向None

删除节点有一个叶子节点（节点的度为1）

只有一个叶子节点时，用叶子节点代替本节点的位置

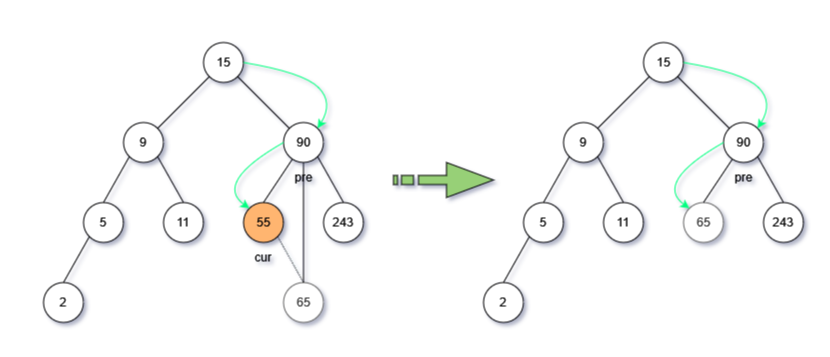
删除节点有两个叶子节点（节点的度为2）
有两个叶子节点时，删除当前节点后，还需要找到替代当前节点的元素。根据搜索二叉树的特点，有两种替代方式：右子树的最小节点或左子树的最大节点
- 右子树最小节点：右子树沿着最左边一路向下最底部节点
- 左子树最大几点：左子树沿着最右边一路向下最底部节点

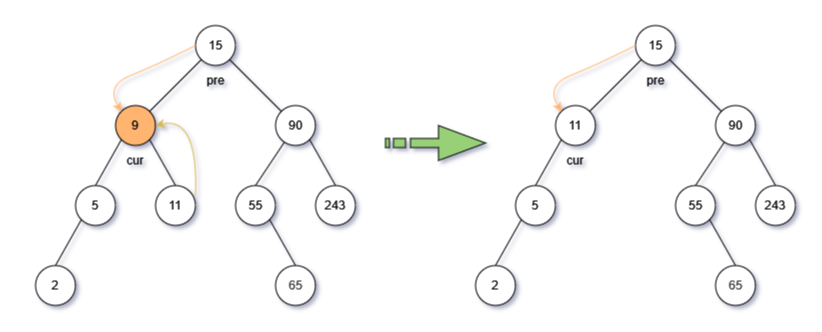
代码实现流程
1. 判断二叉树是否为空None，如果为空，返回False，肯定是无法删除元素；
2. 深度优先方式遍历二叉树，找到待删除的元素，中断while循环；如果未找到待删除的元素，此时cur=None
3. 当未找到待删除元素时，返回False，也是无法删除元素的；
4. 处理只有0、或者一个子树情况：
  1. 先获取子节点（可能为None或者是一个节点），然后进行两层判断，先判断待删除元素是否为根节点，然后判断子节点是左、右节点，
  2. 替换相应的节点
  3. 处理有2个子树情况：
  4. 找到右子树的最小节点，通过while循环走到右子树的最左边底部，获取此节点；
    1. 删除此节点（将父节点的这个指针指向None，已经最底部了，值可能为None）
  5. 替换节点内容：cur.val=tmp.val
5. 此时，全部流程处理完毕，该返回False的两种情况已经处理，且节点已经删除或者替换，返回True。

# 删除元素，删除成功返回True，失败返回False
    def remove(self,value)->bool:
        # 首先判断树是否为空
        if self.__root is None:
            return False
        cur=self.__root
        pre=None

        # 遍历二叉树，查找待删除的元素
        # 找到元素跳出循环，否则继续循环，直到二叉树遍历结束
        # 注：如果未找到元素，此时cur=None，找到元素时，cur=该元素，而pre则为父节点
        while cur is not None:
            if cur.val==value:
                break
            pre=cur
            if cur.val<value:
                cur=cur.right
            else:
                cur=cur.left

        # 遍历结束仍未找到要删除的元素
        if cur is None:
            return False
        # 找到待删除的节点，判断节点子节点的个数
        # 有0、1个子节点时
        if cur.left is None or cur.right is None:
            # 获取叶子节点
            child=cur.left or cur.right
            if cur!=self.__root:
                if pre.left==cur:
                    pre.left=child
                else:
                    pre.right=child
            else:
                self.__root=child
        # 有2个子节点时，这里是将右子树最小节点代替删除节点内容
        else:
            tmp=cur.right
            # 退出while循环时，tmp位于子树最左侧节点，即最小节点
            while tmp.left is not None:
                tmp=tmp.left
            # 此时tmp为叶子节点，直接删除即可。
            self.remove(tmp.val)
            cur.val=tmp.val
        return True

五、全部代码

from collections import deque
from typing import Optional


class TreeNode:
    def __init__(self, val: int):
        self.val: int = val
        self.left: Optional[TreeNode] = None
        self.right: Optional[TreeNode] = None


class BinaryTreeSearch:
    def __init__(self):
        self.__root: TreeNode = None
        self.__res=[]

    # 广度优先遍历
    def bfs(self):
        self.__res=[]
        queue = deque()
        queue.append(self.__root)
        while queue:
            node: TreeNode = queue.popleft()
            self.__res.append(node.val)
            if node.left is not None:
                queue.append(node.left)
            if node.right is not None:
                queue.append(node.right)
        return self.__res

    # 深度优先搜索
    # 这一段是看了别人的写法，很有意思
    # 注意if判断的位置和含义
    def dfs(self,node,order):
        cur = node
        if node is None:
            return
        if order=='pre':
            self.__res.append(cur.val)
        self.dfs(cur.left,order)
        if order=='mid':
            self.__res.append(cur.val)
        self.dfs(cur.right,order)
        if order=='post':
            self.__res.append(cur.val)

    # 深度优先遍历-中序
    # 中序遍历，应该返回一个有序的列表
    def dfs_mid(self):
        cur=self.__root
        self.__res=[]
        self.dfs(cur,'mid')
        return self.__res

    def dfs_pre(self):
        cur=self.__root
        self.__res=[]
        self.dfs(cur,'pre')
        return self.__res

    # 当value> 当前节点，跳至当前节点的右子节点
    # 当value< 当前节点，跳至当前节点的左子节点
    # 在while循环中，如果相等则返回True，如果while循环结束仍未跳出循环，说明未找到，则在while循环外返回False
    def search(self, value)->bool:
        cur = self.__root
        while cur is not None:
            if cur.val < value:
                cur = cur.right
            elif cur.val > value:
                cur = cur.left
            else:
                return True
        return False

    # 考虑两种情况，数为空None和非空，为空则建立一个新节点，然后root指向即可
    # 树非空时，则根据搜索的原理，沿着路径向下走，直到空节点（cur），此时pre为父节点
    # 判断value与pre节点的大小，然后在左右插入节点。
    def insert(self, value):
        if self.__root is None:
            self.__root=TreeNode(value)
            return
        cur=self.__root
        pre=None
        while cur is not None:
            if cur.val==value:
                return
            pre=cur
            if cur.val<value:
                cur=cur.right
            else:
                cur=cur.left

        node=TreeNode(value)
        if pre.val<value:
            pre.right=node
        else:
            pre.left=node

    # 删除元素，删除成功返回True，失败返回False
    def remove(self,value)->bool:
        # 首先判断树是否为空
        if self.__root is None:
            return False
        cur=self.__root
        pre=None

        # 遍历二叉树，查找待删除的元素
        # 找到元素跳出循环，否则继续循环，直到二叉树遍历结束
        # 注：如果未找到元素，此时cur=None，找到元素时，cur=该元素，而pre则为父节点
        while cur is not None:
            if cur.val==value:
                break
            pre=cur
            if cur.val<value:
                cur=cur.right
            else:
                cur=cur.left

        # 遍历结束仍未找到要删除的元素
        if cur is None:
            return False
        # 找到待删除的节点，判断节点子节点的个数
        # 有0、1个子节点时
        if cur.left is None or cur.right is None:
            # 获取叶子节点
            child=cur.left or cur.right
            if cur!=self.__root:
                if pre.left==cur:
                    pre.left=child
                else:
                    pre.right=child
            else:
                self.__root=child
        # 有2个子节点时，这里是将右子树最小节点代替删除节点内容
        else:
            tmp=cur.right
            # 退出while循环时，tmp位于子树最左侧节点，即最小节点
            while tmp.left is not None:
                tmp=tmp.left
            # 此时tmp为叶子节点，直接删除即可。
            self.remove(tmp.val)
            cur.val=tmp.val
        return True


if __name__ == "__main__":
    arr = [15,9,90,5,11,55,243]
    bts=BinaryTreeSearch()
    for val in arr:
        bts.insert(val)
    bts.insert(2)
    bts.insert(65)
    print('广度优先遍历：',bts.bfs())
    print('搜索一个元素：',bts.search(55))
    print('深度优先搜索-中序：',bts.dfs_mid())
    print('深度优先遍历-前序',bts.dfs_pre())
    print(bts.remove(9))
    print('2.广度优先遍历：', bts.bfs())
    print('2.深度优先搜索-中序：', bts.dfs_mid())

Python二叉搜索树操作

Python二叉搜索树操作

一、遍历二叉树

二、搜索节点

三、插入节点

四、删除节点

五、全部代码

results matching ""

No results matching ""

results matching ""

No results matching ""