Python排序算法-归并排序
归并排序,类似于快排,也是通过递归实现的一种排序算法。
- 实现思路:
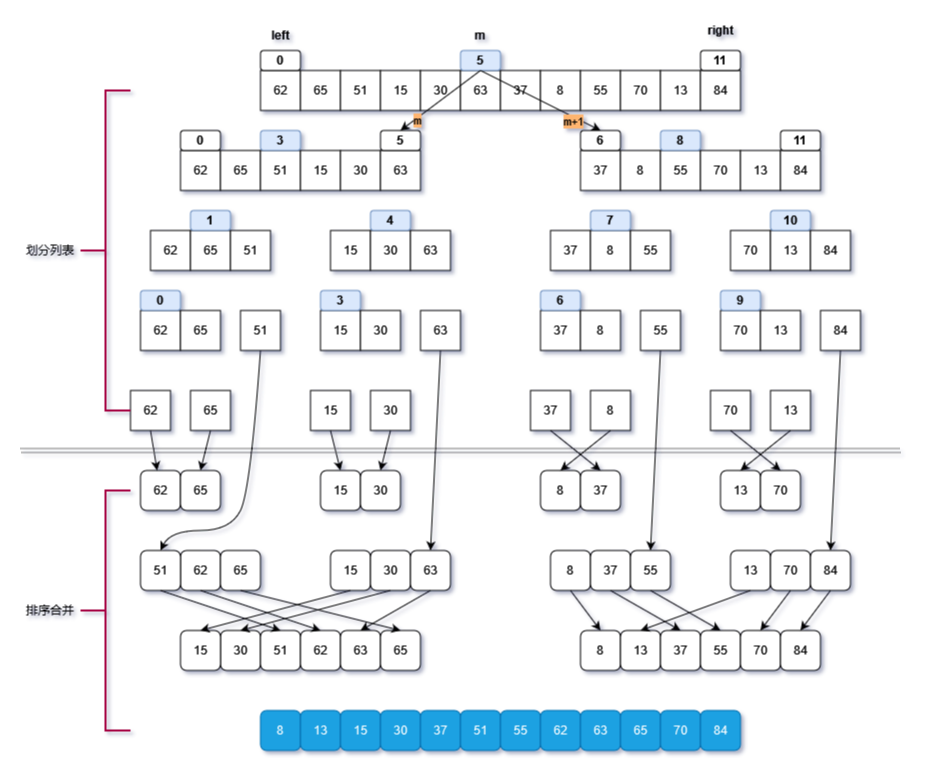
归并排序算法思路上分为两个步骤:划分列表和排序合并列表。
- 划分列表:通过递归的方式,将列表从中间位置,划分为左、右子列表,直到子列表的长度为1,然后向上返回。
- 排序合并列表:在左、右子列表划分长度为1时,在向上递归返回时,对左右子列表进行合并排序,并填入原列表中。
- 实现步骤:
列表的长度为n,即列表所有元素的表示范围为:
[0,n-1],对最左、右侧元素下标分别命名为left,right划分阶段,通过左右下标,计算列表中间位置,下标命名为mid,即此时有列表的3个下标lefe,mid,right,分别代表列表的左,中间,右元素的下标,通过不断递归调用自身,直到列表的长度为1,达到递归函数的边界(终止)条件返回。
排序合并阶段:对左右子列表进行排序,先定义一个临时列表tmp,比较左右子列表,从小到大填入tmp列表:
while i <= mid and j <= right: if nums[i] <= nums[j]: tmp[k] = nums[i] i += 1 else: tmp[k] = nums[j] j += 1 k += 1如果左右子列表有部分元素较大,然后通过while循环,将子列表元素全部填入tmp临时列表:
while i <= mid: tmp[k] = nums[i] i += 1 k += 1 while j <= right: tmp[k] = nums[j] j += 1 k += 1将临时列表tmp元素填入原列表nums
- 注意要点
划分左右子列表是,注意左列表最右侧元素(mid)和右子列表最左侧元素(mid+1)的下标。必须要包含mid元素。
划分左右子列表的递归边界条件是子列表长度为1,即无法划分系列表。
if left >= right: return合并排序列表时,临时列表tmp填入原列表nums,注意起始下标从left开始,子列表长度从小到大,从从左子列表起点left开始,保证左右子列表均能填入nums
- 代码:
# 归并排序
# 合并函数,对分解的列表,合并排序存储在tmp列表中,然后将列表中元素复制到nums中
def merge(nums: list[int], left, mid, right):
tmp = [0] * (right - left + 1)
i, j, k = left, mid + 1, 0
# 合并左右子列表,从左端逐个比较左右列表,然后按序存入tmp列表
while i <= mid and j <= right:
if nums[i] <= nums[j]:
tmp[k] = nums[i]
i += 1
else:
tmp[k] = nums[j]
j += 1
k += 1
# 对左右子列表仍有元素未插入的(即大的元素,存入tmp列表尾部)
while i <= mid:
tmp[k] = nums[i]
i += 1
k += 1
while j <= right:
tmp[k] = nums[j]
j += 1
k += 1
# 将临时列表数据存入nums列表中,并且保证位置(下标)对应
for k in range(0, len(tmp)):
nums[left + k] = tmp[k]
# 归并排序,使用递归方式,先处理左右子列表,当列表元素为1时,向上返回,然后使用合并排序函数merge进行排序
def merge_sort(nums: list[int], left, right):
# 递归边界条件(终止):判断列表元素是否为1
if left >= right:
return
mid = (left + right) // 2
# 分别处理左右子列表
merge_sort(nums, left, mid)
merge_sort(nums, mid + 1, right)
# 子列表排序合并
merge(nums, left, mid, right)
if __name__ == "__main__":
nums = [62, 65, 51, 15, 30, 63, 37, 8, 55, 70, 13, 84, 46, 44, 86, 11, 91, 10, 47, 3, 96, 9, 36, 54, 24, 72,
29, 45]
merge_sort(nums, 0, len(nums) - 1)
print(nums)
`