Python二分查找算法

二分查找算法的前提条件是列表是有序的。

本次实现以双闭区间表示的方式，这种方式更容易理解，而且在写代码时，不容易因为下标计算转换以及while循环跳出时出错。

双闭区间表示方法：

• 最左侧下标为：left_index，起始从0开始
• 最右侧下标为：right_index，起始从len(list)-1，即要包含最右侧的元素
• 中值下标为：m=(left_index+right_index)//2，向下取整

实现方式

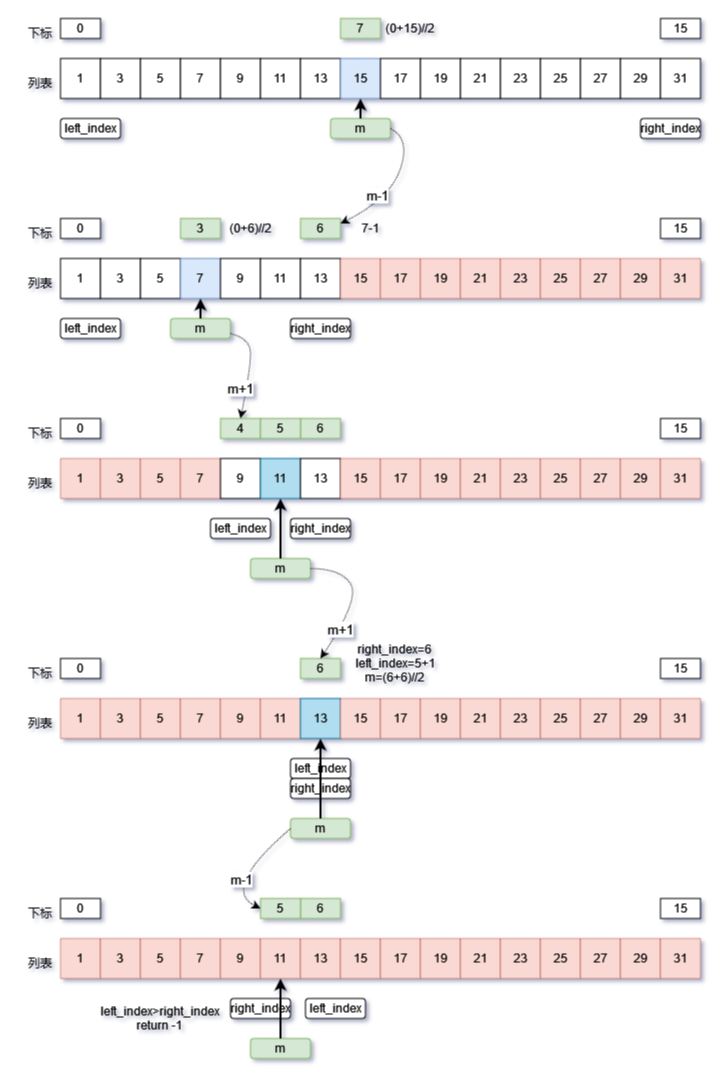
通过在循环中不断移动左右侧下标的值，缩小查找的范围，直到右侧下标小于左侧下标，终止循环，退出查找，或者找到对应的元素，退出查找。

• 如果目标值小于中间值：nums[m] > num，调整最右侧的下标为：right_index = m - 1，进入列表左侧继续查找，此时区间为[left_index,m-1]
• 如果目标值大于中间值：nums[m] < num，调整最左侧下标为：left_index = m + 1，进入列表右侧继续查找，此时区间为[m+1,right_index]
• 如果目标值等于中间值，则返回列表的下标
• 如果继续循环遍历，列表中没有找到对应的目标值，最左右侧的效标通过不断的变化，先会出现left_index=right_index，然后下一次循环就会left_index > right_index，最后跳出while循环。

这里需要注意几点：

• 每次进入循环后，是已经调整左右侧下标值，然后计算中间下标；
• 调整左或右侧下标时，是不包含原中间侧下标的值，因此是m+1，或者m-1
• while循环经过不断调整左右侧下标，没有找到元素时，右侧下标会小于左侧下标
• 重点注意：while循环比较的是while left_index <= right_index:，这里用的是<=，因为未找到元素时，会出现left_index <= right_index，如果用<符号，则无法比较到最右侧下标的值。这就是双闭区间与左闭右开方式的区别。

# 二分查找，左右双闭方式
def binary_search(nums: list[int], num: int):
    left_index, right_index = 0, len(nums) - 1
    # 必须是<=，否则无法查找到最左、右侧的元素
    while left_index <= right_index:
        # 每次循环，均先调整左右边界的列表下标，然后计算中间值下标
        print('在[{}]至[{}]中查找'.format(left_index,right_index))
        m = (left_index + right_index) // 2
        if nums[m] < num:
            left_index = m + 1
        elif nums[m] > num:
            right_index = m - 1
        else:
            return m
    return -1

左闭右开区间表示法

通常左右均为闭区间，较为方便，但是左闭右开也是一种表示方式。由于右侧是开区间（即不包含最右侧下标的这个元素），因此最右侧下标的移动方式略有不同。

• 左右侧的起始为：left_index,right_index=0,len(list)，即比较的时候，不能包含最右侧的下标元素（越界）
• 如果目标值小于中间值：nums[m] > num，调整最右侧的下标为：right_index = m，进入列表左侧继续查找，此时区间为[left_index,m)
• 如果目标值大于中间值：nums[m] < num，调整最左侧下标为：left_index = m + 1，进入列表右侧继续查找，此时区间为[m+1,right_index)
• while循环中，由于不包含最右侧下标的元素，因此应该为：left_index<right_index。